A 3D-s képalkotási eljárások, fogalmak

Ezt a fejezetet egy fogalmi átvezetőnek képzeltem el az első kettő fejezet és azt követők között. A fejezet olyan fontos ismereteket tárgyal, amelyek nélkül az ezt követőek nem igazán érthetőek meg. Elsőként szeretném bemutatni azokat az eljárásokat, algoritmusokat, amelyek segítségével létre hozhatóak a 3D-s képek. Elsőként a geometriai műveletvégzésről írok. A második alfejezetben a textúrázáshoz kapcsolódó szűrési és árnyalási algoritmusok bemutatását tervezem. Az utolsó alfejezetben, pedig a pixel fillrate és a látható kép meghatározásához szükséges két fontosabb algoritmust mutatom be.

 Itt szeretném felhívni a figyelmet a diplomamunka végén lévő Függelék című részre, ahol abc rendben gyűjtöttem össze a fontosabb fogalmakat, amelyeket meglátásom szerint ismernie kell annak, aki 3D-s kártyát akar vásárolni. Olyan megnevezések is vannak közöttük, amelyekkel a kártyagyártók jellemzik saját grafikus kártyáinak a teljesítményét.

3.1 Geometriai számítások, műveletvégzés

A háromdimenziós világban lévő objektumokat a megjelenítéshez sokszögekre (poligonokra) kell felbontani. A poligonok PC-s platformon szinte mindig háromszögek (esetek 99%-ában). Az adott objektum megjelenítése a gyakorlatban az objektumot alkotó háromszögekkel történő műveletvégzést jelenti (transformation, ligthing, triangle setup). Meg kell határoznia a központi processzornak, vagy a geometriai társprocesszornak a háromszögek csúcspontjainak az elhelyezkedését.

A számítógépes grafikában megkülönböztetjük a koordinátatranszformációt és a ponttranszformációt (bővebb leírás a Függelék „Fogalmak” című alpontjában található). A ponttranszformációk közül a grafikában az ún. affin transzformációkat használjuk. Ezek az eltolás, forgatás, mozgatás, nagyítás/kicsinyítés, összenyomás/széthúzás. Az alábbi ábra a különböző ponttranszformációkat szemlélteti, amelyeket összefoglaló néven affin transzformációnak nevezünk.

16. ábra: affin transzformációk

Az objektumokat alkotó háromszögek mérete és száma tetszőleges lehet, természetesen a megjelenítő hardveregység fizikai korlátait figyelembe véve. Egy összetett, változatos formákból álló alak megjelenítéséhez sok apró háromszögre van szükség, mint ahogy a 17. ábra is mutatja. A jobb oldali ábrán látható kerék sok kicsi poligonból épül fel. Ezáltal sokkal szebb, kidolgozottabb képet kaptunk a virtuális világban.

17. ábra: látható a különbség a két kerék között

3.2 Textúrázás

A háromszögekre felbontott modelltérbeli objektumokat 2 dimenziós képekkel a szó legszorosabb értelmében fel kell őket „öltöztetni”, így nyerik el külsejüket. Vagyis 2D-s képeket vetítünk a 3D-s felületre oly módon, hogy megtaláljuk az éppen feldolgozott pixelhez illő texelt.

Ennek folyamán az adott képkocka minden egyes képpontja (pixel) meghatározásra kerül, méghozzá általában több texel (adott textúra egyetlen képpontja) kombinálásából.

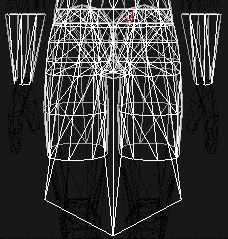
18. ábra: objektum drótváza (bal) és a textúrázott objektum (jobb)

Különböző eljárások léteznek az objektumok textúrázására, szűrésére.

3.2.1 Szűrő és képjavító eljárások textúrázás során

Bilineáris szűrés

Ennél a metódusnál a pixel színének meghatározásakor nem csak a közvetlenül odaillő texelt vesszük alapul, hanem a mellette lévőket is, és végül e négy színérték átlagolásával határozzuk meg a textúra egy képpontjának a színét. Vagyis meg kell találni a két legközelebbi texelt mind a két dimenzióban és a súlyozott átlagukat kell kiszámítani. Mind horizontálisan, mind vertikálisan keressük a 2 legközelebbi texelt. Így többé-kevésbé meg lehet akadályozni a textúra szétesését, azonban a pixelesség helyébe homályosság lép. Ezért tűnnek el, vagy homályosodnak el az objektumok, ha közelítünk hozzájuk.

   20. ábra: Point sampling és a bilineáris szűrés összehasonlítása

MIP mapping

 A latin Multum In Parvum (sok kicsiben) rövidítése ez a metódus. Gyakorlatilag ez a megoldás az adott textúra előre elkészített, bilineárisan szűrt, kicsinyített változatai. Így ki lehet küszöbölni a megnövekedett sávszélesség-igényt, hisz a bilineáris szűrés egyetlen pixel színének meghatározásához négy altexelt használt.

21. ábra: MIP mapping

MIP-map-ek egyébként nem csak ebből a szempontból hasznosak. Akkor is fontos szerepük lehet, ha például egy textúrát távolról látunk. Ekkor ugyanis nem kell feltölteni a memóriába a teljes textúrát, hanem elegendő valamelyik megfelelő MIP-map-et - így is csökkentve a sávszélesség-igényt.

A bilineáris szűrést és a MIP-map-eket rendszeresen kombinálják. A közelebbi képeknél a bilineáris szűrést használják, míg a távoliaknál a MIP-map metódust.

Trilineáris szűrés

A két MIP-map szint közötti váltás nagyon durva, feltűnő. Erre jelent megoldást a trilineáris szűrés. A pixel színének meghatározásához vesz 4 altexelt a textúrától való távolságra nézve legcélszerűbb MIP-map-ből, majd vesz 4 altexelt a második legcélszerűbb MIP-map-ből is, s az így kapott 8 altexel színét átlagolja egy texellé. Megkeresi a két legközelebbi pixelt mindkét dimenzióban, majd a két legközelebbi MIP-map-ben.

Kevesebb képhiba, ugyanakkor nagyobb homályosság és sávszélesség-igény jellemzi. Egy texel színének meghatározásához 8 altexelre van szükség.

Anti-aliasing(élsimítás)

 A megjelenítés során gyakran kell ferde és görbe vonalakat rajzolni. A monitoron a  görbe vonalak szélei szükségszerűen fűrészfogasan jelennek meg. Az antialiasing eljárás ezeket a fűrészfogakat próbálja meg kiegyenesíteni pixelenkénti mintavételezéssel úgy, hogy a görbe vonal mellé olyan képpontokat helyez, amelyek átmenetet képeznek a háttérbe, így a ferde vonalak szélei sokkal simábbnak látszanak. Minél nagyobb felbontásban dolgozunk annál kisebbek a képpontok, annál kevésbé feltűnő a fűrészfogazottság a vonalak széle mentén, így kevésbé van szükség erre a technikára. Ezt a technikát, ha a teljes képre használják, akkor Full Scene Anti-aliasing-nak nevezik (FSAA).

Multitexturing

A pixel színének meghatározásához két textúrában is megkeressük az odaillő texelt, s az így kapott két színt átlagoljuk egy színné. Az eljárás lehetővé teszi a processzor, vagy a geometriai társprocesszor tehermentesítését. Sík területre alkalmas ligtmap-ek (fénytérképek), amik voltaképp csak elsötétítik, vagy kivilágosítják az összemosást követően az alaptextúrát, így imitálják a fényhatásokat.

+ =

                        22.ábra: alapkép+ fénytérkép= megvilágított kép

3.2.2 Árnyalási algoritmusok

A multitexturing elsősorban síkfelületek megvilágítására alkalmas. Az árnyalás legegyszerűbb formája a flat shading. Minden egyes poligonhoz csak egy fényerő-értéket számítunk, ami meghatározza az egész háromszög megvilágítását. Ennek előnye, hogy nem terheli le a processzort, de ugyanakkor a kapott hatás nem a legjobb, a poligonok közötti határvonalak élesen látszanak a hirtelen fényerő-váltásnak köszönhetően.

Henri Gouraud dolgozta ki azt az eljárást, ami napjainkban használatos. A Gouraud shading kiszámíttatja a háromszög mindhárom csúcspontjának fényerejét, majd azok interpolálásával határozza meg a köztes területek megvilágítását. Az 23. ábrán látható a flat shading és Gouraud shading eljárások által nyert hatás különbözősége.

23. ábra: flat shading és Gouraud shading

A Gouraud shading akkor alkalmazható, ha a háromszögön belül a szín valóban közelítőleg lineárisan változik. Ez igaz a diffúz visszaverődésű objektumokra, de nem megfelelő a tükrös illetve spekuláris visszaverődésű felületekre.

A legjobb módszer az árnyalás problémájának megoldására a Phong shading. Minden egyes pixelnek külön-külön határozza meg a fényerejét. Értelemszerűen ezzel valósítható meg a legtökéletesebb, legpontosabb megvilágítás, ugyanakkor a 3 bemutatott árnyalási módszer közül ez a leginkább erőforrás-igényes.

A Gouraud- és a Phong-modell közötti különbség leglátványosabban a fényfoltok megjelenítésében különbözik. Azonban nem csak a fényfoltok megjelenítésében van közöttük különbség, hanem a kedvezőbb eredményt általában a Phong-shading nyújtja.

Köd

A programok a grafikus gyorsító, illetve a processzor véges teljesítőképességére való tekintettel csak bizonyos távolságig alkotják meg a háromdimenziós világot. Egy objektum az egyik pillanatban még épp kívül esik azon a bizonyos távolságon, ám a következő percben átlépi a határt, és váratlanul megjelenik. E probléma áthidalására szolgál a határvonal közelében lévő köd, mely lényegében elfedi a hirtelen előtűnést, hiszen amikor felbukkan az objektum, akkor a köd miatt nem látszik, és csak szép lassan, fokozatosan jelenik meg, ahogy közeledik.

Ködöt, mint előforduló természetes jelenséget fotorealisztikus képen is kell ábrázolni. Ekkor a ködnek megfelelő színt (ez általában a fehér vagy halványszürke színeket jelenti) a nézőponttól távolodva egyre nagyobb arányban keveri a pixelekhez, texelekhez.

A ködhöz hasonlóan a fotorealisztikus képen a füstöt és az átlátszódást is meg kell jeleníteni. A füstöt általában egy speciális textúrával modellezzük. A füstnek megfelelően kell mozgatni az ábrázoló textúra elemet. Ezek a textúra elemek részben elmosódottak, részben átlátszóak.

Az átlátszóság megjelenítésénél figyelembe kell venni a fénytörést, a diffúz áttetszőséget és a fény intenzitásának csökkenését az átlátszó testen. Átlátszóság modellezésére jó példa az ötödik alfejezetben mért Far Cry nevű játék. Itt a víz alól látható a „szárazföldi táj” teljes egészében, vagyis a víztükör teljesen átlátszó. 

Alpha blending

Az alpha blending elnevezésű technika szolgál az átlátszó hatások előállítására. Alpha blending eljárás használatos üveg, füst, köd, pára és víz megjelenítésekor. Az átlátszó kép minden egyes pixele kap egy úgynevezett „alpha” értéket, amely meghatározza, hogy az eredeti pixellel való összemosáskor melyik pixel színe mekkora súllyal szerepel.

24. ábra: alpha blending

LOD (Level Of Detail)

A messzeségbe vesző sokszögeknek nem kell, hogy részletesen ki legyenek rajzolva, hiszen ezeket egyébként úgysem látjuk annyira tisztán, mint a közelieket. Ezáltal a kártya az egyéb feladatra (bonyolult számításokra) jobban tud összpontosítani. A LOD a távolabbi objektumokat kevesebb sokszögből építi fel, amire később kisebb felbontású textúrákat feszít. Az eltérő sokszögszámú tárgyak között átmenet van, hogy a változás szembetűnő ne legyen.

3.3 Látható kép meghatározó algoritmus (z-buffer)

Az elkészült (textúrázott és effektezett) pixelek a grafikus kártya memóriájában, illetve annak egy kifejezetten e célból elkülönített részében, a frame buffer-ben (képkocka puffer) állnak össze egy képpé. A hardver azonban itt sem marad feladat nélkül. A 3D gyorsítók túlnyomó többsége ugyanis mindmáig úgy dolgozik, hogy a modelltér objektumait feldolgozzák. Ez viszont nyilvánvalóan nem csak a részben, vagy egészben takarásban lévő tárgyaknál felesleges, hanem egy tárgynak is értelmetlen minden oldalát megalkotni, hiszen a játékos úgyis csak egy bizonyos szemszögből látja. A chip poligonról poligonra halad. Vesz egy háromszöget, feldolgozza a hozzá tartozó pixeleket, majd a képkocka pufferbe írja őket. Ezután veszi a következő háromszöget, annak pixeleit is feldolgozza, majd a képkocka pufferbe küldi őket. Vagyis még mindig nem dőlt el, hogy mi a látható és mi nem.

3.3.1 Z-buffer

A Z-buffer feladata, hogy minden feldolgozott pixelhez rendeljen egy úgynevezett mélységi értéket. Amikor egy új pixel kerül a képkocka pufferbe, akkor a 3D gyorsító összehasonlítja annak a mélységi értékét a kép azonos pontján már meglévő pixelével. A Z-buffer képpontos algoritmust már 1974-ben Catmull kidolgozta, azonban még 2 évtizedet kellett várni, hogy költséghatékonyan megvalósítható legyen.

Két tárolóterületet vesz igénybe, az un. frame buffert (képernyő pixeljeihez rendelt színértéket tárolja) és a z-buffert (egyes pixelekhez rendelt z értékeket tárolja normalizált látótérből). A mélységtároló algoritmus minden egyes normalizált látótérbeli objektumára végrehajtásra kerül:

∙ egy tetszőlegesen kiválasztott (x, y) koordinátákkal rendelkező pixelhez tartozó vetítősugárhoz kiszámítjuk az összes általa metszett objektumhoz tartozó értéket.

∙   amikor egy új pixel kerül a képkocka pufferbe, akkor a 3D gyorsító összehasonlítja annak a mélységi értékét a kép azonos pontján már meglévő pixelével. Ha az új pixel Z-értéke kisebb (tehát lényegében közelebb áll a szemlélőhöz), akkor az új pixel felülírja a régit. Ha viszont nagyobb (magyarán az új pixel a régi mögött helyezkedik el), akkor a képkocka pufferben nem történik semmi változás (az új pixel gyakorlatilag elveszik).   

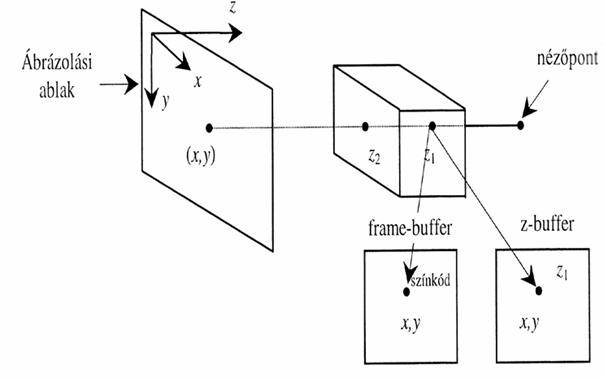
25. ábra: z-buffer algoritmus elve

Valahányszor megkezdünk egy új képkockát, ezt a két buffert (frame buffer, z-buffer) ki kell üríteni. Ez több-kevesebb időt igényel, ami alatt a 3D gyorsító tétlenül várakozik, és nem dolgoz fel egyetlen pixelt sem. Ám hogy ez pontosan mennyi időt jelent, az három dologtól is függ: a memória típusától, a kép felbontásától (minél nagyobb a felbontás, annál több memóriát kell üríteni) és természetesen a frame rate-től, azaz attól, hogy másodpercenként hány képkocka kerül megjelenítésre. Természetesen szoftveres trükkökkel az ürítés szüksége eliminálható, ám ez az adott alkalmazástól függ.

A z-buffer algoritmus a modelltér elemeinek formájától független, így sokféle felület (poliéder, görbült) láthatóságának megállapítására alkalmas. Formától független, viszont ismernünk kell az objektumok felületi pontjaiban a nézőponttól való z távolságot és az árnyalási információkat. 3D-s gyorsítókártyákban könnyen realizálható. Hátrányai közé tartozik, hogy jelentős erőforrásigénnyel rendelkezik.

3.3.2 Scan-line

A Scan-line algoritmus képpontosság műveleteket használva, pixelsoronként készíti a képet. Alapja a poligonok frame bufferbe történő soronkénti konvertálásása. A Scan-line algoritmus nagy előnye, hogy az objektumok közötti geometriai összefüggéseket figyelembe veszi. Így képes a látható pixelek meghatározásához szükséges tesztelésekből a feleslegeseket kiszűrni. Például, ha két egymást követő pixelsorhoz tartozó aktív élek és ezek sorrendje megegyezik, akkor nem történik változás az objektumok takarási viszonyaiban, vagyis nem szükséges a poligonok (háromszögek) újabb mélységi vizsgálata.

3.3.3 Pixel fillrate

A pixel fillrate azt fejezi ki, hogy egy másodperc alatt hány pixelt képes feldolgozni az adott videokártya. Számítása elméletben roppant egyszerű: a 3D gyorsító chip órajelét megszorozzuk a teljes értékű pixel pipeline-ok számával. Vagyis egy órajel alatt hány pixelt képes elkészíteni az adott termék. 26. ábra szemlélteti az általam kiválasztott videokártyák adatait.

26. ábra 12 grafikus kártya pixel fillrate táblázata

A táblázatban látható adatok csak elméleti maximumot mutatnak, amely azt feltételezi, hogy a 3D gyorsító valamennyi órajelét pixelek előállítására fordítja. A gyakorlatban azonban ez nincs mindig így.

Adott körülmények között a következő három tényezőtől függ, hogy elvileg mekkora pixel fillrate kellene:

∙ Felbontás. Egyetlen 1024x768-as felbontású képen például 786,432 pixel van

∙Depth complexity. A z-pufferekben felesleges munkavégzés is történik. Ezt a jelenséget jellemzi a depth complexity (mélységi összetettség). Ha ennek értéke például 3, akkor ez azt jelenti, hogy a 3D gyorsító az adott programban rendszerint háromszor annyi munkát végez (háromszor annyi pixelt dolgoz fel), mint amennyi ténylegesen felhasználásra is kerül.

∙Frame rate. A másodpercenként megjelenített képkockák száma.

Visszalépéshez kattints a képre!